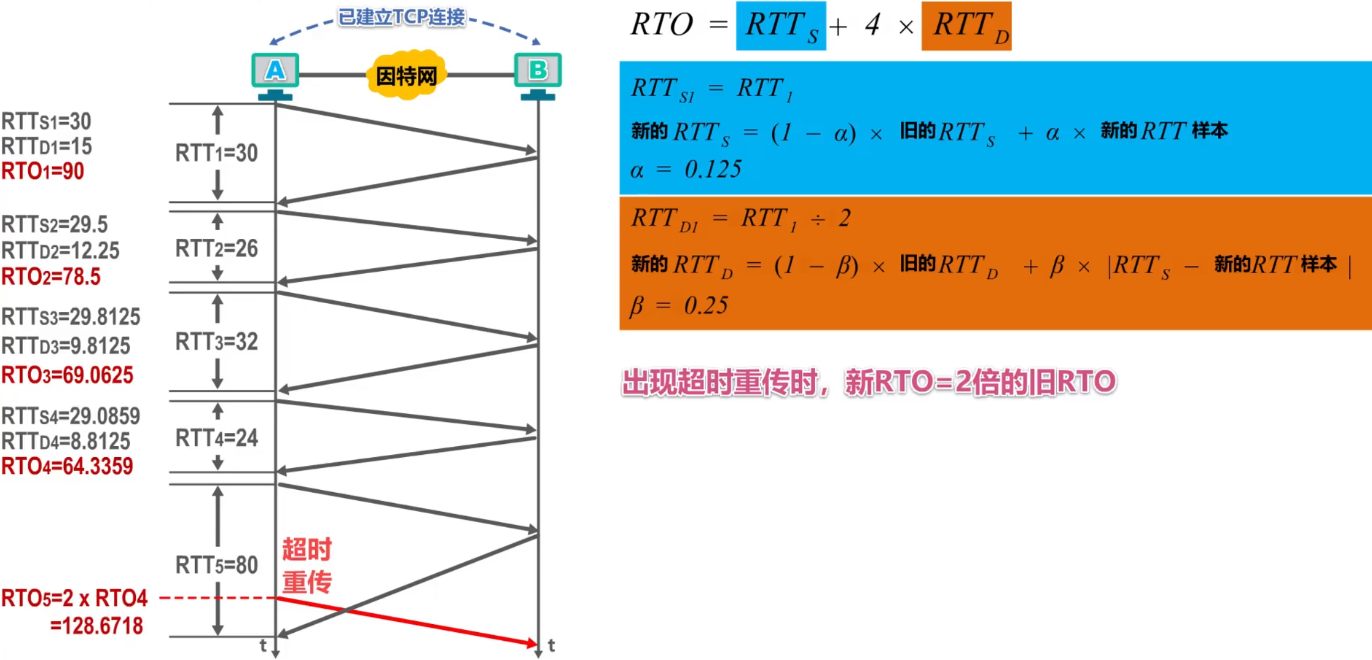
TCP超时重传时间的选择

超时重传时间的选择是TCP最复杂的问题之一

不能直接使用某次测量得到的RTT样本来计算超时重传时间RTO。

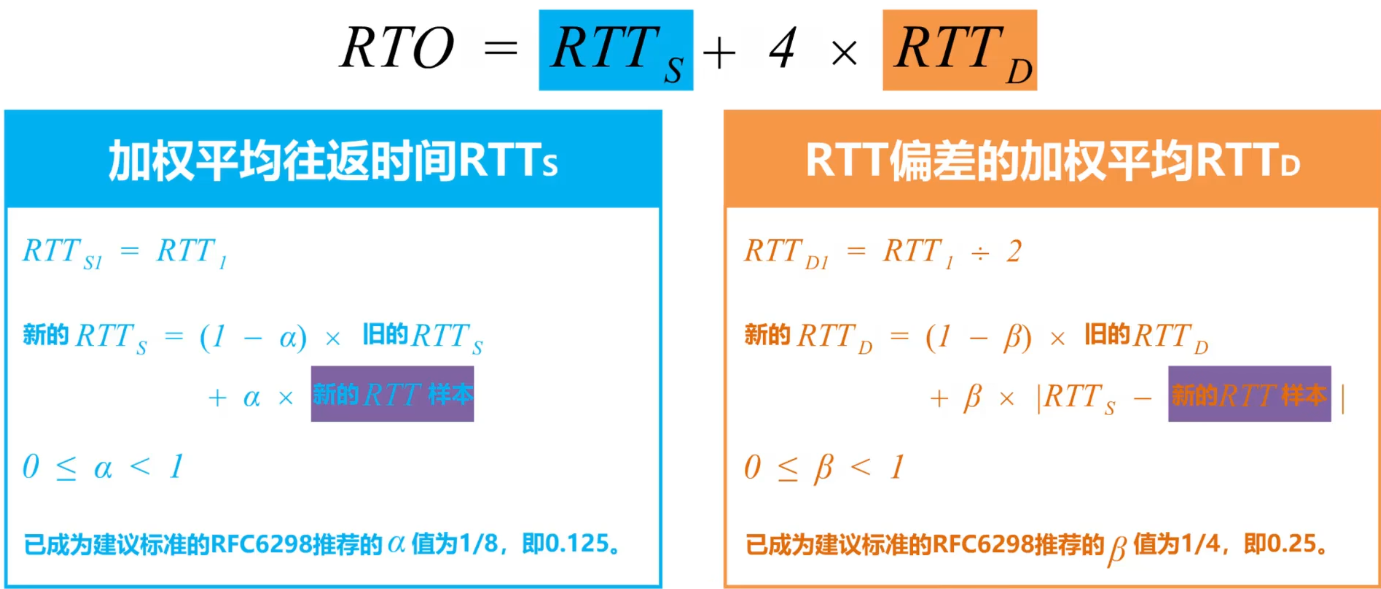
利用每次测量得到的RTT样本，计算加权平均往返时间RTTs（又称为平滑的往返时间）。

RTTs = RTT1

新的RTTs = (l - α) ×旧的RTTs+α ×新的RTT样本

在上式中,0 ≤a <1 :

若α很接近于0，则新RTT样本对RTTs的影响不大;

若α很接近于1，则新RTT样本对RTTs的影响较大;

已成为建议标准的RFC6298推荐的α值为1/8，即0.125。

用这种方法得出的加权平均往返时间RTTs就比测量出的RTT值更加平滑。

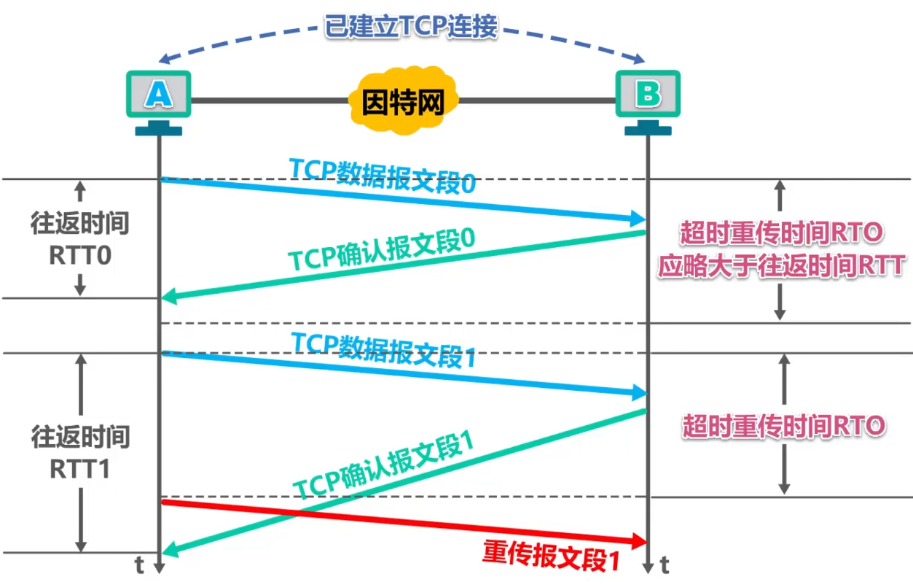
显然，超时重传时间RTO应略大于加权平均往返时间RTTs。

RFC6298建议使用下式计算超时重传时间RTO:

往返时间RTT的测量比较复杂

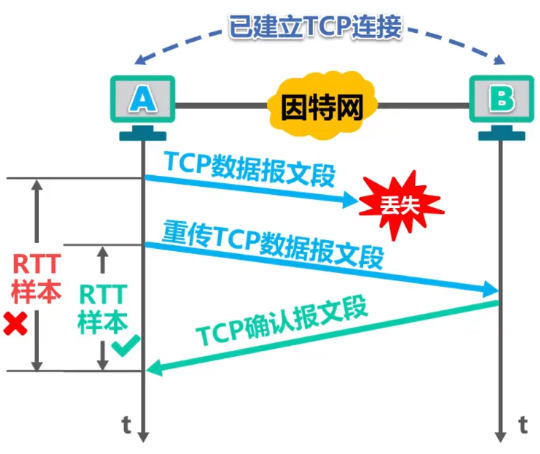
源主机若误将确认当作是对原报文段的确认:

所计算出的RTTs和RTO就会偏大，降低了传输效率;

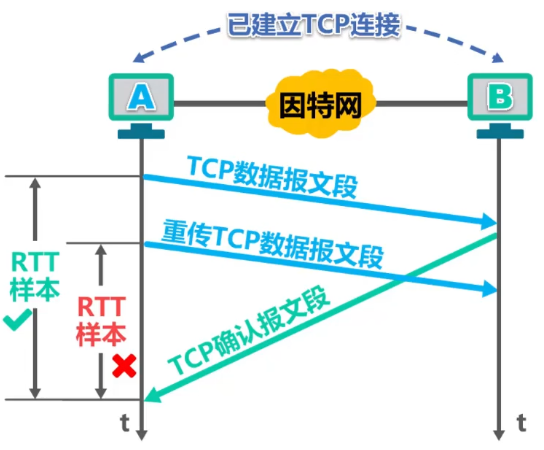
源主机若误将确认当作是对重传报文段的确认：

所计算出的RTTs和RTO就会偏小，导致报文段没必要的重传，增大网络负荷;

针对出现超时重传时无法测准往返时间RTT的问题，Karn提出了一个算法:在计算加权平均往返时间RTTs时，只要报文段重传了，就不采用其往返时间RTT样本。也就是出现重传时，不重新计算RTTs，进而超时重传时间RTO也不会重新计算。

这又引起了新的问题。设想出现这样的情况:报文段的时延突然增大了很多，并且之后很长一段时间都会保持这种时延。因此在原来得出的重传时间内，不会收到确认报文段。于是就重传报文段。但根据Karn算法，不考虑重传的报文段的往返时间样本。这样，超时重传时间就无法更新。这会导致报文段反复被重传。

因此，要对Karn算法进行修正。方法是：报文段每重传一次，就把超时重传时间RTO增大一些。典型的做法是将新RTO的值取为旧RTO值的2倍。